[Strategy Market] GC Vs GU in stacks

[paramodic]

Before I continue, my apologies if this has been mentioned before.

So, while playing around in challenge mode, something caught my attention: The Uracil in GU pairs hates the Cytosine in GC pairs when they’re stacked close together. Observe the target shape and the stack of multiple GU pairs here: http://eterna.cmu.edu//sites/default/…

And when a GC pair is introduced, a disruption- consistently forming a 2-2 internal loop- appears immediately afterwards, as seen here: http://eterna.cmu.edu//sites/default/…

This will even occur if the GC pairing at the bottom of the visible string is switched, as seen here: http://eterna.cmu.edu//sites/default/…

Consistently, when there are >2 GU pairs following a GC pairing, if the cytosine is on the Uracil side, a disruption occurs. However, there are some exceptions. If the GC pair is not at least three NT’s from the ‘end’ of the string (marked by the 1NT bulge), the anomaly does not occur, as seen here: http://eterna.cmu.edu//sites/default/…

Tampering with the system appears to indicate that the direction the anomalous activity treats as forward or downstream hinges upon which side the Uracil is placed on. If the Uracil is placed on the left, as in my example, the anomaly consistently occurs superior (north) to the GC pair placement. If the Uracil is on the right, the anomaly occurs in the inferior (south) direction. Also, when the Guanine in the GC bond is on the Uracil side, no special activity occurs. As seen here: http://eterna.cmu.edu//sites/default/…

Playing around with this, I’ve found that one can be successful in the attempt of stabilizing an intentional 2-2 internal loop in this fashion. AU pairs appear unphased by cytosine.

So, for each GC pairing with C in line with the U’s of multiple downstream GU in a stack, deduct a point.

[Edward_Lane]

I wondered if this might be important int he conversation that was being held about 2-2 loops ?

[JeehyungLee]

Dear paramodic,

Your strategy has been added to our implementation queue with task id 104. You can check the schedule of the implementation here.

Thanks for sharing your idea!

EteRNA team

[paramodic]

Yeah, Edward

[JeehyungLee]

Sorry paramodic - I was replying very late at night : [ It’s fixed now!

[paramodic]

It’s okay, I was just poking fun, Jee.

[paramodic]

In one puzzle I was just playing, I made an internal 2-2 loop with a negative energy value of -4.2 Kcal that way, so I’m thinking this is going to be a powerful way of supporting internal loops.

[paramodic]

This should help clear things up, I think. Thanks to Eli Fisker for the idea. The sequence I’m using is: AGUCAAUUUUGAUUUUUUAAUUGAUUUUUUUUUGAGACGAAAAAACGACACGGGGGGGGGCAAUAUGGGGGGACGGGGGGGACAAAAA

And here we go. Here’s the strand in its native state:

Now I’ll let the pictures take it from here.
Note that it doesn’t really matter where the GC pair is placed, as long as it’s > 3 NT’s from the downstream end of the string and the cytosine is on the same side as the Uracil.


Eli Fisker will also be following up with a post of his own soon. I hope this clarifies what I’m talking about a little.

[paramodic]

Click on the pictures to enlarge them. I didn’t mean for them to be so small. T_T"

[drake178]

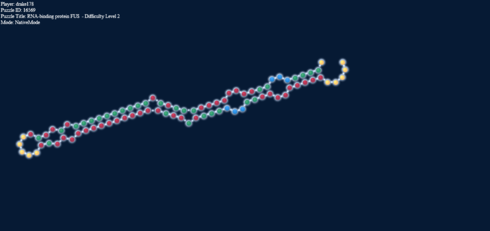
I’ve explored upstream G downstream C a bit for you, here’s the picture:

The energies (excluding the tetra) are -3.1; -4.4; -4.2; did’t fold; -3.5; -2.1; -2.5; -3.5; -1.1; -2.5, the strongest being with another G-C in the end in the same direction.

Notice the one in the middle didn’t fold out. The two triplets on the right can repeat the last loop ad infinitum. An interesting side note is that i’ve put this sequence into RNAshapes and RNAfold and they predict an entirely different bulging (to this one and to each other). Here’s the sequence if you want to look for yourself:

AGGGUGGGGUUGGGUGGUGUUGGAUGGCUGGGUGGGUGGGUGACUGUCUGCCUGGCUGUCUGAUGUUGUCUGGUUUUGUUUAAAAAAA

Edit: here’s some A-U starters, first two upstream U, the rest upstream A:

Energies: -2.5; -2.5; -2.5; -2.9; -2.9; -2.5; -1.6; -2.5; -3.5; -3.5; and that could turn into infinite -2.5s too.

The two on the left are the only ones that formed with upstream U, with the second being capable of infinite looping. If you switch the G-C pair in the last one on the right, the looping stops there unless you switch some G-Us further on too.

One thing i can think of is that alternating G-U pairs have positive energy instead of negative and your RNA will want to get out of that ASAP, in effect the pairs individually attract each other, but their middles probably keep colliding and pushing apart, resulting in a bulge that is neither a connection nor a loop really.

Next picture, Gs and Us on the same side of the loop, Us upstream:

Energies: -1.2; -1.1; -3.5; -3.1; -3.5; didn’t fold; -1.6; didn’t fold

The two on the right were the only ones that formed with A-U, both needed an alternate G-U on the other end compared to the loop itself, same goes for the one that formed up on the right. This might explain why the other two on the right didn’t form up, they had A-U on the other end with no G. The only real puzzles are the two in the middle, the ones with all G-Us the same way, the single G-C doing what paramodic explained in the above post.

Even if all the above phenomena could be traced back to the alternate G-Us repulsing each other, this last one would not really be explained by that. All of these loops have negative total energies meaning that unlike regular loops which must be “forced” into shape by surrounding stacks these loops will in fact sustain themselves, and not only that they strengthen the surrounding structures too, letting you use weaker pairs around them and still sustain the shape. The real question is whether they behave the same in nature as say a 2-2 Adenine only “forced” loop or do they look and taste completely different?

And here’s a bit more:

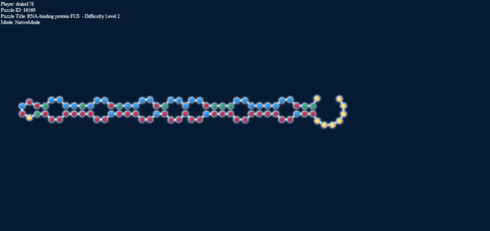
Energies: -3.5; -1.1

The thing to notice here is that the bulge goes towards the alternating G-U regardless of the G-C present this way, to eliminate the positive loop energy that would result from that. With some G-C and A-U pairs you can force out those pairs (loop energies +0.3 and +1.3) but they will want to get away from each other no matter what.

These loops can take quite the strain too:

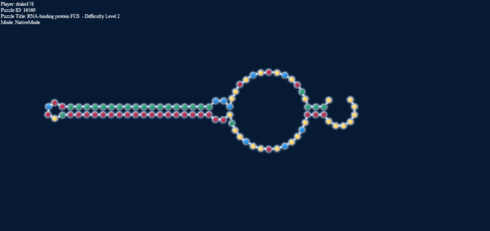
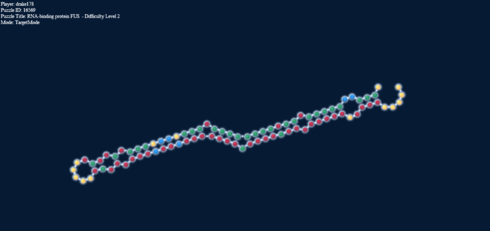
Here’s another interesting thing. The two pictures below, one in target mode with a 2-2 loop and one in natural mode without it have exactly the same energy.

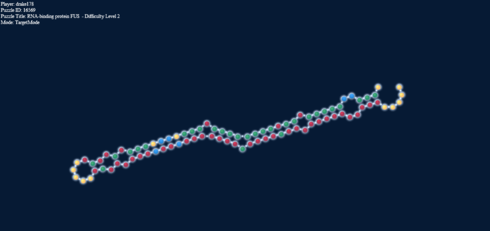
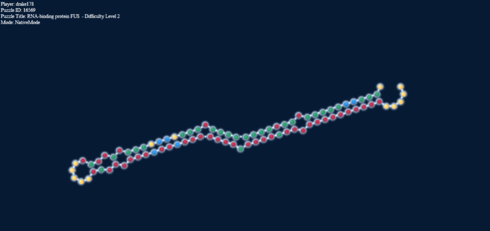
Loop energy = Paired energy = -4.1

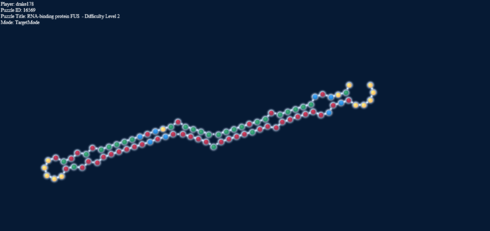
That is, the connections formed net the same energy as the loop would. I know what you’re going to say, that would likely be the case for anything. Well, it isn’t. Here:


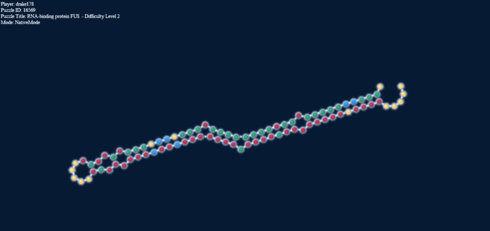
Loop Energy = +2; Paired energy = -5.1

But to add more to this, here’s something else: on the right we have a loop, and in the left stack, forced into target mode the identical base pairs:

Loop energy = -2.2; Paired energy = +0.1 (!)

I’ve checked a few others and they all seem to line up to the same rule, so the real question is why those G-U loops provide a greater net negative than the sum of their parts. I assume the secret lies in knowing how exactly the formed pairs relate to the bases forming right next to them. From my experience downstream double G is a stretcher for example, link a C to the first and the second will stabilize any split in the stack starting with the second G. And obviously once you’re in the middle of a strand upstream really is only downstream looked from the other side, so everything will work both ways:

[Eli_Fisker]

Paramodic wished that I read his post with his strategy GC Vs GU in stacks. I had forgotten as I was busy writing other posts. But he found just the right words to make me take a look: But I think you’ll find that it fits right in with your ideas on energy jumps causing destabilization.

He walked me through the puzzle he was playing with in his strategy and what he thought he have found.

What Paramodic demonstates above in his post, is that somehow a whole string does not like to have a complete long line of blue and green on a string. Especially not if a lot of the pairs are GU-pairs. And that it has an effect which way they turn.

It was him making me reverse all the GU-pairs as he does in the last picture of the post, that made me see the light. I discovered that the structure slided, when I switched between natural and target mode. Let me show you.

Target mode

You can mark nucleotides with holding Ctrl down and clicking on them with the mouse.

Now watch this slide happening. You can see that the marked nucleotides are no longer above each other.

Natural mode

Paramodic did say it might be related to energy gaps, here is the relation I see. I have marked the energy gaps. It did slide, and I think the energy gaps at the ends caused it. And the slide opens the structure at exact those three spots where there is an energy gap.

Energy gaps from the left
1: 0.4 + -1,7 = -1.3
2: -2.1 + -0.5 = -1.6
3: -0.5 +2.4 = -1.9

Watch the energy at gapside after the slide:

Energy gaps from the left
1: 0.8 + -2.1 = -1.3
2: -2.1 + -0.5 = -1.6
3: -0.6 + -2.1 = -2.7

Having too long lines of green and blue in a string and lines of green close to multioop I knew was bad, but I hadn’t connected it to energy gaps. But I think the energy gap causes things to slide in this structure. I’m not sure what it means that the energy gap got bigger after the slide and not smaller as I expected. But I think the inner loop forming in the puzzle had a stabilizing effect. In lab it will not be possible for this 2-2 loop to form like this, as we know it’s occourance is currently a flaw in the algorithm EteRNA is working on .

It was Paramodics effort to make me read it that made me connect the dots.

Here is the puzzle in question

Fill it out like this to see the effect.